Post archives
Filtering for posts tagged with ‘NUKEMAP’
Showing 1-22 of 22 posts that match query
2022
April 2022
News and Notes
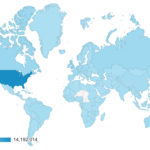
An accounting of NUKEMAP traffic for the first few months of 2022, including the massive spike in usage during the Russian invasion of Ukraine.
February 2022
Meditations
NUKEMAP was released into the world a decade ago, believe it or not.
2019
December 2019
News and Notes | Visions
The top-secret story of why NUKEMAP switched from Google Maps to Mapbox+Leaflet.
2018
January 2018
News and Notes
Reflections on the end of 2017, and the start of a new nuclear year.
2017
July 2017
News and Notes
Announcing a new, provocative venture at the Stevens Institute of Technology, for building the next-generation of nuclear risk communication.
February 2017
Visions
Reflections on the past, present, and future of NUKEMAP, five years into its existence.
2015
August 2015
Meditations
Seven decades later, how do we talk about the atomic bombs?
2013
December 2013
Meditations
What airburst physics tells us about nuclear targeting decisions, and why it took so long for the NUKEMAP to support arbitrary burst heights.
August 2013
Meditations | Visions
I thought I knew a lot about nuclear fallout, but digging into the details taught me some subtle but important points about how it worked.
July 2013
Visions
Two new photoessays about the first atomic bomb and its creators.
News and Notes | Visions
The new NUKEMAPs are up!
News and Notes
NUKEMAP2 and NUKEMAP3D are now online!
News and Notes | Visions
A teaser for the things to come.
June 2013
Redactions | Visions
Making sense of the worst radiological accident in US history.
May 2013
Meditations
Of the $2 billion spent on the Manhattan Project, where did it go, and what does it tell us about how we should talk about the history of the bomb?
February 2013
Meditations
Why I get annoyed when we talk about meteors, earthquakes, and tsunamis in terms of megatonnage.
News and Notes | Visions
Some data from a year of NUKEMAP, and a promise of new things to come...
2012
June 2012
Visions
Thoughts on attempts to re-capture the horror of a nuclear explosion.
February 2012
News and Notes | Visions
Reflections on the "explosive" success of NUKEMAP, and answering some questions about it that I've seen floating around.
Visions
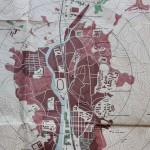
A proto-NUKEMAP from 1950 tried to help industrialists assess their risk from atomic warfare.
Meditations
New NUKEMAP features, plus a discussion of the first 1,500 "detonations."
Visions
A new tool for demonstrating the qualitative effects of nuclear weapons.
Showing 1-22 of 22 posts that match query